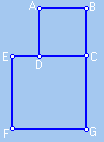

Traçamos o segmento BE e as retas r e s perpendiculares à EB passando, respectivamente,
pelos pontos E e B. Seja H o ponto de r sobre o segmento FG. Traçamos a reta
perpendicular à EH passando por H e seja I o ponto de intersecção
desta reta com s. Traçamos IJ perpendicular à BG.
As cores nos indicam como transformar os dois quadrados dados, ABCD e ECGF,
no quadrado maior BEHI.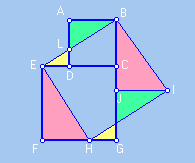
 Polígono transformado em quadrado
Polígono transformado em quadrado Volta à Apresentação
Volta à Apresentação